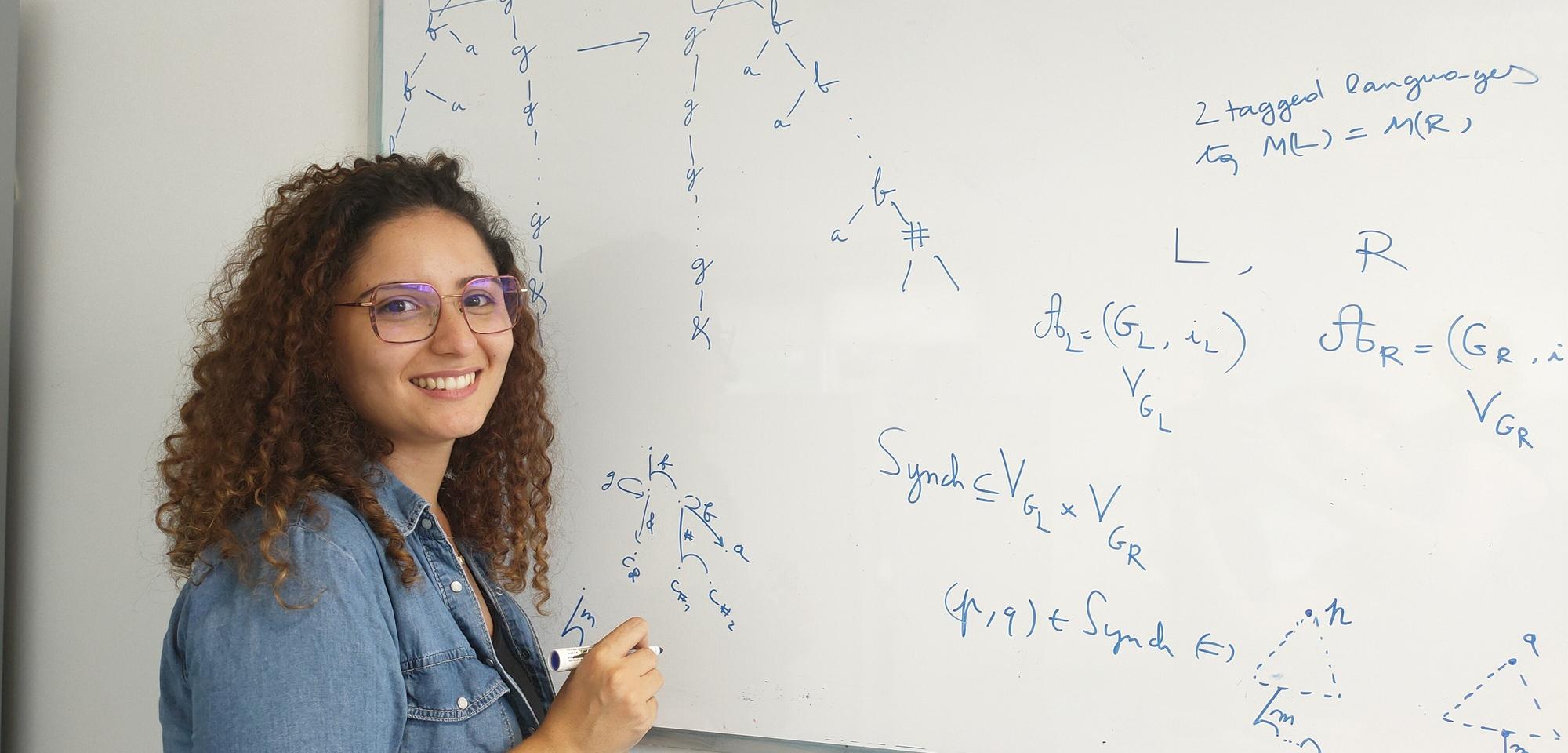
Les chercheurs
Sirine BOUDABBOUS
UN PROGRAMME INFORMATIQUE S’ARRÊTE T-IL ? OU TOURNE T-IL INDÉFINIMENT ?
Sirine BOUDABBOUS est une jeune chercheuse en Informatique théorique au sein du laboratoire LIM (Laboratoire d’Informatique et de Mathématiques) de l’Université de La Réunion. Elle fait partie de l’équipe de vérification de programmes, qui vérifie qu’un programme respecte certaines propriétés particulières, telles que l’absence et la présence de bugs. L’une des activités majeures, sur laquelle Sirine travaille, est de déterminer si un programme informatique se termine ou non dans le but de s’assurer qu’il ne tourne pas indéfiniment et donc que ce programme est fiable.
Sirine travaille sur des systèmes de réécriture. Ces derniers permettent en informatique de modifier des expressions selon certaines règles. Par exemple, deux règles peuvent être de dire «si tu vois ‘C’, remplace-le par ‘M’» et si tu vois “MI” remplace le par “ S”. Le mot “CIEL” devient ainsi “MIEL” et “MIEL” peut à son tour devenir “SEL”.
Mais on ne peut pas réécrire le mot «MAISON» parce que «C» et «MI» n’y sont pas.
Un langage est un ensemble de mots. À partir d’un mot de départ, on peut créer un langage en suivant les règles du système de réécriture.
Les langages les plus simples, dits “réguliers”, peuvent être reconnus par un automate. C’est-à-dire une machine à laquelle on donne un élément en entrée et qui renvoie une sortie.
Sirine cherche à décider si un programme s’arrête ou non en étudiant les propriétés de systèmes de réécritures particuliers. En partant d’un langage reconnu par un automate et en appliquant des règles de réécriture, tombons-nous sur un nouveau langage lui-même reconnu par un automate ? L’ensemble des couples de mots issus d’une réécriture est-il reconnu par automate ?
Son travail consiste à démontrer mathématiquement ces propriétés. Sirine travaille sur papier munie de son crayon en suivant l’intuition acquise par le travail répété sur des exemples et par des lectures d’articles de chercheurs du même domaine, ce qui lui demande une attention minutieuse et une analyse méthodique.
Fiche publiée en 2026.
- Montrer la préservation de la régularité de certains systèmes de réécriture.
- Développer un outil logiciel qui permettra de décider de la terminaison de programmes et d’en dégager des propriétés mathématiques.


